Расчет коэффициента амбиполярной диффузии.

Нами был проведен расчет коэффициента диффузии электронов и дырок в слое сульфида мышьяка для двухслойной пленки, при экспонировании светом с длиной волны 380 нм, когда практически весь свет поглощается в селенсодержащем слое. Для выполнения условия электронейтральности расчет коэффициента диффузии проводили для случая n/=p/, когда диффузию носителей обоих типов можно рассматривать аналогично амбиполярной диффузии [13] в газах и плазме. Для случая n/=p/ в полупроводнике происходит не независимая диффузия электронов и дырок, а диффузия пар электрон – дырка. В нашем случае диффузия электронов и дырок определяется общей характеристической длиной (длина диффузионного смещения - x), одинаковой для электронов и дырок. Считая, что диффузия носителей в нашем случае характеризуется общей эффективной подвижностью электронов и дырок, и временем экспонирования, в течение которого происходит диффузия, коэффициент диффузии рассчитывался по формуле [13]:

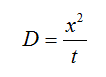где t – время экспонирования, x – длина диффузионного смещения.

Расчет коэффициента амбиполярной диффузии, проводился для слоя сульфида мышьяка в двухслойной пленке при облучении селенсодержащего слоя светом с длиной волны 380 нм. За величину диффузионного смещения электронов и дырок в слое сульфида мышьяка принимали расстояние вглубь слоя сульфида мышьяка, при котором значение селективности травления было равно 2. Ниже приведена зависимость длины диффузионного смещения от времени экспонирования. Из полученных данных мы получили, что коэффициент амбиполярной диффузии для этого случая равен (5±3)*10-15 см2/сек.

Величину полученного коэффициента амбиполярной диффузии, можно сравнить с величиной коэффициента диффузии, рассчитанной из данных по дрейфовой подвижности. Согласно уравнению Нернста – Эйнштейна коэффициент диффузии и подвижность связаны между собой соотношением:

В литературе имеются данные по величине дрейфовой подвижности электронов в стеклообразном сульфиде мышьяка [14]. При 450 С она равна 10-10 см2/(В*с). Рассчитанная из полученных нами данных величина дрейфовой подвижности самых медленных носителей заряда (электронов) равна 10-11 см2/(В*с), что хорошо согласуется с литературными данными.